employee from 01.01.2002 until now
Russian Federation
employee from 01.01.2005 until now
National Research University of Electronic Technology (Institute of Systems and Software Engineering and Information Technology (SSEIT), associate Professor)
employee from 01.01.2005 until now
Zelenograd, Moscow, Russian Federation
UDC 371.315.3
UDC 53
In this work, it is argued that modern students are more susceptible to academic stress than their predecessors. Objective: to improve the efficiency of student learning. Task: to reduce the level of anxiety among students at the initial stages of studying the theory of errors.
didactics, propaedeutics, adaptation of educational content, methodological support of the educational process of the university, laboratory practice in physics, physics experiment, approaches to error estimation, theory of errors
Art. ID: m06s03a10
Введение. О некоторых особенностях современной системы образования
Термин «современный», как мы знаем, имеет двоякое значение. С одной стороны, этим термином одобрительно характеризуют соответствие кого-то или чего-то вызовам, моде, насущным потребностям той или иной современности. С другой, это может быть всего лишь констатацией того, что рассматриваемое явление или объект является частью этого «настоящего времени» — и в этом случае характеристика не всегда подразумевает одобрение. В нашем случае «современность» будем трактовать именно в этом ключе — осознавая и отчасти принимая реалии сегодняшней системы образования и кондиции приходящих в университеты абитуриентов.
Своей статьей мы хотим привлечь внимание образовательного сообщества к актуальности практикуемого в XX в. подхода к введению в теорию погрешностей. В наши дни применение этого подхода с некоторыми дополнениями помогает преодолевать ощутимый разрыв между школьными знаниями и требованиями вуза, а также формировать у студентов-первокурсников умение самостоятельно проводить эксперименты, обрабатывать результаты и учитывать погрешности до изучения специальных разделов математики. По нашему мнению, такой подход позволяет обеспечить вовлеченность всех студентов, не допуская блокирующего познавательную активность страха непонимания, неудачи.
Формулировка проблемы
Отметим, что одной из ощутимых проблем современности для преподавателей физики в вузах является сохранение внешних ожиданий/требований к уровню/результатам подготовки студентов научных и инженерных специальностей при произошедших довольно существенных переменах — как в задачах страны, так и в «спецификациях» первокурсников «эры ЕГЭ».
В частности мы имеем дело со следующими обстоятельствами:
- Если раньше поступающие на технические направления обязательно должны были сдавать физику, причем на высоком уровне — что считаем логичным, если учесть ее важность для освоения инженерных дисциплин, — то теперь вузы предоставляют право участвовать в конкурсе абитуриентам, сдавшим физику или информатику, и считают результаты ЕГЭ по этим предметам равно значимыми [1]. Например, в НИУ МИЭТ этот принцип действует уже порядка пяти лет. В 2025 г. такой выбор доступен для 16 из 17 «технических» направлений [2]. Подобная ситуация наблюдается и в правилах приема, действующих в МФТИ [3].
- У студентов «не физических» специальностей технических направлений нет достаточной для изучения «непрофильной» дисциплины мотивации, так как в обществе многие настроены на получение сугубо тех навыков, которые могут привести к выгодному трудоустройству при минимизации личных трудозатрат.
- Современные студенты сильнее, чем их предшественники, подвержены учебному стрессу — «состоянию, характеризующемуся чрезмерным напряжением тела, снижением эмоционального и интеллектуального потенциала, что в конечном итоге приводит к психосоматическим заболеваниям и задержке личностного развития студента» (Семенова, 2019), цит. по: (Чербиева, Бостанова, 2019). В своей работе С. В. Чербиева и С. Н. Бостанова к причинам такого стресса отнесли: не сданные вовремя и не защищенные работы, большое количество пропусков, нехватку знаний, отставание по предмету; большое количество заданий для выполнения в короткий срок; отсутствие интереса к дисциплине; возникновение конфликтных ситуаций с преподавателем; отсутствие учебных материалов; неудовлетворенность полученной оценкой; разочарование по поводу выбранной профессии (Чербиева, Бостанова, 2019: 447).
- Кроме того, разумеется, необходимо учитывать иные значимые факторы снижения эффективности когнитивной деятельности, актуальные для нашего времени, — например, отраженные в работе (Ященко, 2023).
При этом одинаковая для всех специальностей в НИУ МИЭТ вводная лабораторная работа по курсу «Физика», направленная на обучение обработке результатов измерений и оценке погрешностей (Горбатый и др., 2015: 5; Спиридонов и др., 2021: 5), подразумевает, как минимум:
- знание частных производных;
- готовность к лабораторным работам в принципе.
По обоим условиям, характеризующим готовность студента выполнять лабораторную работу без предварительной подготовки (т. е. по «входным требованиям»), которые, пользуясь терминологией SWOT-анализа (Харач, 2015), назовем «W» (т. е. «слабые стороны»), мы легко обнаруживаем следующие «T» (т. е. «источники угрозы») для относительно благополучного освоения необходимого учебного материала (цели):
- Действующая сейчас школьная программа по математике (базовый уровень) не предусматривает изучение частных производных и более сложных математических методов — статистики и дифференциального исчисления, необходимых для полного понимания теории погрешностей и обработки экспериментальных данных в том режиме, к которому были готовы поступившие в вуз более десяти лет назад [4].
- В наши дни лабораторные работы проводят не во всех школах или классах — это следует из фактической материально-технической и кадровой обеспеченности.
Изучение физики в высших учебных заведениях по сложившейся традиции начинается с механики. Соответственно, студенты-первокурсники НИУ МИЭТ начинают знакомство с лабораторным практикумом по курсу общей физики «Механика» с помощью одного из методических учебных пособий, разработанных с учетом технической оснащенности вуза, возможностей доступного студентам экспериментального оборудования (Горбатый и др., 2015; Спиридонов и др., 2021).
Однако проведенный нами анализ методической литературы подтвердил предварительную гипотезу о том, что на протяжении порядка трех десятков лет — даже при переоснащении лабораторий и модернизации учебных пособий в разных вузах (МИЭТ, МАИ, СПбГУТ, УрФУ, ВГУ, НИЯУ МИФИ, УрГПУ) — вводная лабораторная работа, посвященная обработке результатов измерений, переходит в обновленные издания практически без изменений — см.:
- МИЭТ (Ткачев и др., 2003; Горбатый и др., 2015; Спиридонов и др., 2021);
- МАИ (Анисимов и др., 2010);
- СПбГУТ (Андреев, Черных, 2009);
- УрФУ (Степанова, Скулкина, Волегов, 2014);
- ВГУ (Голицына, Меремьянин, Рисин, сост., 2015);
- МИФИ (Леонтьева, Лисицын, 2015);
- УрГПУ (Русанов, Сидоров, 2023).
Переступая порог лаборатории в первую неделю своего обучения в вузе, вчерашние школьники, как и их предшественники, сталкиваются с необходимостью вычислять стандартные отклонения, строить доверительные интервалы и анализировать погрешности измерений, используя частные производные. Только, в отличие от предшественников, в наши дни многие обучающиеся не готовы к описанным процедурам ни интеллектуально, ни эмоционально. И перед преподавателями встает дополнительная задача: либо организовать/инициировать мероприятия, компенсирующие пробелы в предшествующем обучении, либо — насколько это возможно — упростить/адаптировать преподносимый мате риал.
Данная задача усложняется тем, что речь идет о первой работе, когда уровень реальной подготовки и стрессоустойчивости обучающихся еще не известен — и личный контакт со студентами еще не сформирован. То есть на стадии предварительного планирования учебной деятельности преподаватель вынужден прогнозировать состояние готовности студентов, опираясь на средние баллы поступивших и понимая специфику системы современного школьного образования.
Вопрос взаимосвязи времени, необходимого на обучение недостаточно подготовленных студентов, и решений, принимаемых в таких ситуациях преподавателями и студентами, более подробно рассмотрен в работе (Бойков, Харач, 2024).
Из описанных в указанной публикации сценариев преподаватели физики при проведении лабораторных работ чаще сталкиваются с двумя:
A. Студент не выдерживает внезапной для него нагрузки, решает, что игнорирование проблемы проще, чем ее решение. Невнимание кураторов/тьюторов к подобной ситуации может повысить число должников и отчисленных за неуспеваемость.
B. Студент перекладывает работу на кого-то, до кого может «дотянуться», — ищет, где / у кого списать, заказывает решение у зарабатывающих такими услугами. Специфика современности в том, что при таком выборе приоритетным оказывается обращение к нейронным сетям.
Анализ подходов, применяемых для решения аналогичных проблем
В такой ситуации уместно говорить о том, что необходимо корректировать ценностные ориентиры общества, совершенствовать систему подготовки кадров, особенно — о необходимости отказа от подушевого финансирования вузов, приводящего к тому, что они встают перед выбором — обучать в режиме «как есть» или терять часть профессорско-преподавательского состава (в том числе высококвалифицированного), причем нет никаких гарантий его восстановления при изменении ситуации. Однако все мы понимаем, что воплощение этой рекомендации относится к категории сложных решений. Соответственно, быстрого эффекта ожидать не приходится, а подготовка кадров для выполнения стоящих перед нашим государством стратегических задач должна продолжаться.
Сообразно данному пониманию, последуем логике бригады строителей из производственной драмы «Премия» [5]: отделим то, что требует государственного масштаба вмешательства, от тех изменений, для которых достаточно сил и полномочий у преподавателей на местах.
С учетом накопленных нами за последние годы наработок одним из наиболее доступных и при этом эффективных решений считаем следующее: адаптировать методическое обеспечение, используемое при обучении обработке результатов измерений, — а именно скорректировать практикуемые с начала 2000-х гг. методы (Ткачев и др., 2003; Горбатый и др., 2015; Спиридонов и др., 2021) с учетом психологических и когнитивных особенностей современных первокурсников.
Для этого, как ни парадоксально, предлагаем обратиться к опыту советской высшей школы [6], описанному во втором (переработанном) издании «Физического практикума» МФТИ за 1967 г. (Белянкин и др., 1967). Во введении этого издания авторы дают практические указания, необходимые для того, чтобы определять точность полученного результата, не привлекая серьезный математический аппарат. Их подход построен на прозрачном анализе и рассуждениях о том, как были получены экспериментальные данные.
Для скептиков, не вполне приемлющих опыт советской школы, можем привести иные авторитетные (переводные) источники, иностранные авторы которых также выбирают подобный путь — объясняют физическую науку в доходчивой для более широкого круга читателей форме:
- Лайош Яноши (Jánossy Lajos), известный венгерский физик (Яноши, 1968), о книге которого переводчик писал: «Предлагаемая вниманию читателей книга представляет собой изложение методов анализа результатов экспериментальных данных. Естественным математическим аппаратом, необходимым для этого анализа, является теория вероятностей. Однако введение понятий и методов теории вероятностей сделано в книге Яноши своеобразно. Автор, избегая ссылок на математические работы (список важнейших книг по теории вероятностей и математической статистике приведен автором в приложении), вводит все необходимые понятия индуктивно, путем проведения физических аналогий и наглядного обобщения примеров. Теория вероятностей как бы заново рождается на глазах читателей. Разумеется, аксиоматическое построение этой ветви математики и ее история остаются при этом полностью вне рамок книги» (Клепиков, 1968).
- Сандер Бэйс (Sander Bais, Em. Professor of Theoretical Physics, Universiteit van Amsterdam) — в своем рассказе о семнадцати фундаментальных уравнениях физики, начиная с механики Ньютона и заканчивая квантовой механикой, общей и специальной теорией относительности и теорией струн, избегает сложных уравнений (Бэйс, 2013).
Основополагающие принципы предлагаемого подхода
Таким образом, в основу изменения подхода, используемого при введении в теорию погрешностей в работе с современными студентами в первом семестре, выносим два ключевых принципа:
- Теория погрешностей не должна быть пугающим ритуалом, который отбивает у студентов интерес к экспериментам и веру в свои силы. Наоборот, предлагаемый подход должен не только нивелировать пробелы в математической подготовке студентов, но и способствовать формированию культуры проведения эксперимента и обработки его результатов.
- Погрешности — это не ошибки, которые следует скрыть, а информация, которую нужно понять. Лабораторный практикум должен стать площадкой, где студенты учатся не бояться отклонений от ожидаемых результатов, а корректно отрабатывать их.
Результаты исследования. Введение в теорию погрешностей:
методическая разработка для преподавателей и основа раздаточного материала для студентов
С учетом этих принципов вводная часть методических указаний по выполнению лабораторной работы № 1 (Горбатый и др., 2015: 5; Спиридонов и др., 2021: 5) приобретает следующий вид.
Законы механики реализуются в законах движения и равновесия физических тел. Для определения численного значения какой-либо физической величины необходимо сравнить эту величину с эталонной. Операция сравнения определенной величины исследуемого объекта с соответствующей эталонной величиной является измерением. Различают два вида измерений — прямые и косвенные. При прямом измерении значение величины определяется непосредственно с помощью измерительного прибора, шкала которого проградуирована в соответствии с принятой единицей измерения данной величины эталонного образца. Например, при измерении массы некоторого тела устанавливается, во сколько раз измеряемая масса превосходит массу эталонного образца в один килограмм. А окончательный результат экспериментального измерения величины 𝑥 записывают в виде
𝑥 = ⟨𝑥⟩±𝛥𝑥.
Абсолютная погрешность 𝛥𝑥 фактически определяет пределы значения измеряемой величины (𝑥′ = ⟨𝑥⟩ − 𝛥𝑥 и 𝑥″ = ⟨𝑥⟩ + 𝛥𝑥), между которыми заключено ее истинное значение.
Для оценки качества измерения вычисляют относительную погрешность 𝛿𝑥.
Например, результаты измерений двух интервалов времени записаны так:
𝑇1 = (1,25 ±0,08) с;
𝑇2 = (214,54 ±0,08) с.
Абсолютная погрешность для каждого измерения равна 𝛥𝑇 = 0,08 с. Однако видно, что точность измерений большего интервала времени 𝑇2 выше. Чтобы отразить это обстоятельство в записи величины погрешности, вычисляют относительную погрешность:
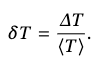
Относительную погрешность называют точностью измерений и часто выражают в процентах, умножая ее полученное значение на 100 %.
В нашем примере:
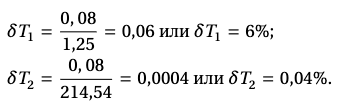
Часто встречается ситуация, когда интересующая нас физическая величина в эксперименте непосредственно не измеряется, но может быть рассчитана с помощью функциональной зависимости от измеряемых величин. Такие измерения являются косвенными.
При косвенном измерении значение искомой величины вычисляют по формуле, включающей результаты прямых измерений. Например, площадь сечения прямоугольного бруска рассчитывается по формуле
𝑆 = 𝑎⋅𝑏,
где длины сторон 𝑎 и 𝑏 определяют прямыми измерениями. Зная погрешности, которые допущены при измерении величин, входящих в результат, можно определить и погрешность самого результата. Точность определения этой величины зависит как от точности эксперимента, так и от конкретного вида ее зависимости от измеряемых величин.
Именно на этапе обработки косвенных измерений возникают трудности, поскольку в современных пособиях просто предлагаются формулы для расчета погрешности с использованием дифференциального исчисления (Горбатый и др., 2015: 8; Спиридонов и др., 2021: 8). Поэтому при обучении теории погрешностей целесообразно использовать доступные и понятные подходы, опирающиеся на простые примеры.
Такой подход способствует более глубокому усвоению материала и эффективной подготовке студентов к самостоятельной работе с экспериментальными данными. На наш взгляд, на этом этапе преподавателю достаточно на конкретных примерах провести вместе со студентами обработку результатов косвенных измерений при сложении (или вычитании), умножении (или делении) величин, степенных, тригонометрических и логарифмических функций. Именно такие функции встречаются в законах, которые проверяют в лаборатории в первом семестре.
Абсолютная и относительная погрешности результата, являющегося суммой или разностью двух величин
Найдем периметр сечения бруска в виде 𝑝 = ⟨𝑝⟩ + 𝛥𝑝, удвоив сумму его длины (⟨𝑥⟩ ± 𝛥𝑥) и ширины(⟨𝑦⟩±𝛥𝑦):
(⟨𝑝⟩ + 𝛥𝑝) = 2((⟨𝑥⟩±𝛥𝑥)+(⟨𝑦⟩±𝛥𝑦)).
Раскроем скобки и перегруппируем слагаемые:
(⟨𝑝⟩ + 𝛥𝑝) = 2(⟨𝑥⟩±𝛥𝑥 +⟨𝑦⟩±𝛥𝑦) = 2((⟨𝑥⟩ +⟨𝑦⟩) ±(𝛥𝑥 +𝛥𝑦));
(⟨𝑝⟩ ± 𝛥𝑝) = 2(⟨𝑥⟩+⟨𝑦⟩)±2(𝛥𝑥 +𝛥𝑦).
Откуда следует, что периметр равен удвоенной сумме его длины и ширины
⟨𝑝⟩ = 2(⟨𝑥⟩ +⟨𝑦⟩),
а его абсолютная погрешность 𝛥𝑝 равна удвоенной сумме абсолютных погрешностей его длины и ширины:
±𝛥𝑝 =±2(𝛥𝑥+𝛥𝑦).
Полученный результат будет справедлив и при вычитании величин: погрешности 𝛥𝑥 и 𝛥𝑦 могут быть любого знака, но их следует рассчитывать, рассматривая самый невыгодный случай.
Таким образом, при сложении (вычитании) некоторых величин складываются их абсолютные погрешности:
(⟨𝑓⟩ ± 𝛥𝑓) = (⟨𝑎⟩±𝛥𝑎)±(⟨𝑏⟩±𝛥𝑏).
±𝛥𝑓 =±(𝛥𝑎+𝛥𝑏).
Относительные погрешности измерений будут выражаться следующими формулами:
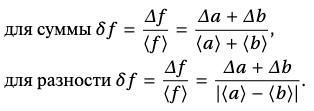
Отсюда следует, что если мы измеряем какую-либо величину, равную разности двух величин, то относительная погрешность тем больше, чем ближе значения измеряемых величин.
Абсолютная и относительная погрешности произведения или частного двух величин
Найдем площадь сечения бруска в виде 𝑆 =⟨𝑆⟩±𝛥𝑆, перемножив его длину (⟨𝑥⟩ ± 𝛥𝑥) и ширину (⟨𝑦⟩±𝛥𝑦):
⟨𝑆⟩ ± 𝛥𝑆 = (⟨𝑥⟩±𝛥𝑥)(⟨𝑦⟩±𝛥𝑦) = ⟨𝑥⟩⟨𝑦⟩ ±⟨𝑥⟩𝛥𝑦±⟨𝑦⟩𝛥𝑥 ±𝛥𝑥𝛥𝑦.
Величиной 𝛥𝑥𝛥𝑦 можно пренебречь, поскольку 𝛥𝑥 и 𝛥𝑦 малы по сравнению с величинами ⟨𝑥⟩ и ⟨𝑦⟩. Для самого невыгодного случая, когда обе погрешности имеют одинаковый знак, получим:
𝛥𝑆 =⟨𝑥⟩𝛥𝑦+⟨𝑦⟩𝛥𝑥.
Вынеся за скобки ⟨𝑆⟩ = ⟨𝑥⟩⟨𝑦⟩, получим:
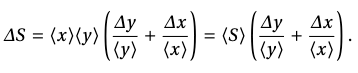
Отсюда:
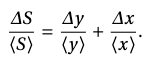
При умножении нескольких величин складываются их относительные погрешности:
𝛿𝑆 =𝛿𝑥+𝛿𝑦.
Аналогичный результат получается при делении величин:
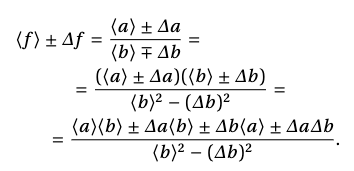
Пренебрежем квадратами и произведением погрешностей. Для самого невыгодного случая, когда погрешности в измерении числителя и знаменателя взяты с обратным знаком, получим:
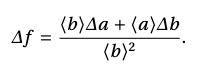
Найдем относительную погрешность:
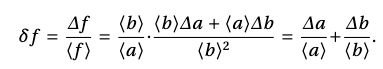
Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя:
𝛿𝑓 =𝛿𝑎+𝛿𝑏.
Таким образом, при умножении и делении величин складываются относительные погрешности.
Абсолютная и относительная погрешность степенной функции
Пусть 𝑓 = (𝑎)2, где 𝑎 — измеряемая величина. Тогда:
⟨𝑓⟩ ±𝛥𝑓 = (⟨𝑎⟩±𝛥𝑎)2,
что соответствует умножению величин:
⟨𝑓⟩ ±𝛥𝑓 = (⟨𝑎⟩±𝛥𝑎)(⟨𝑎⟩±𝛥𝑎),
а следовательно, сумме их относительных погрешностей:
𝛿𝑓 =𝛿𝑎+𝛿𝑎 =2𝛿𝑎,
где 2 — показатель степени.
Аналогичный результат мы получим для степенной функции:
⟨𝑓⟩ ±𝛥𝑓 = (⟨𝑎⟩±𝛥𝑎)𝑛,
где 𝑛 — показатель степени.
Ее относительная погрешность будет равна:
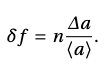
То есть относительная погрешность степени равна относительной погрешности основания, умноженной на показатель степени, а абсолютная погрешность результата равна:
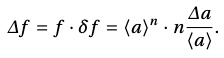
Абсолютная и относительная погрешность тригонометрической функции
Пусть 𝑓 = sin 𝛼, тогда
⟨𝑓⟩ ±𝛥𝑓 = sin(⟨𝛼⟩±𝛥𝛼),
где 𝛥𝛼 — абсолютная погрешность измерения угла. Полагая ввиду малости 𝛥𝛼, что cos 𝛥𝛼 = 1 и sin 𝛥𝛼 = 𝛥𝛼,получим:
⟨𝑓⟩ ±𝛥𝑓 = sin(⟨𝛼⟩±𝛥𝛼) = sin⟨𝛼⟩ ⋅ cos𝛥𝛼 ±cos⟨𝛼⟩ ⋅ sin𝛥𝛼 = sin⟨𝛼⟩ ± cos⟨𝛼⟩ ⋅ 𝛥𝛼,
откуда:
𝛥𝑓 =cos⟨𝛼⟩⋅𝛥𝛼,
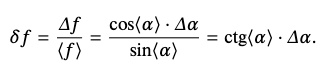
Абсолютная и относительная погрешность логарифмической функции
Пусть 𝑓 = ln𝑏, тогда
⟨𝑓⟩ ±𝛥𝑓 = ln(⟨𝑏⟩±𝛥𝑏),
где 𝑏 — измеряемая величина, а 𝛥𝑏 — ее абсолютная погрешность. Имея в виду, что

откуда:
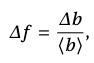
т. е.:
𝛥ln𝑏 = 𝛿𝑏.
Комментарии
В прошлые годы, когда в лаборатории проводили семь четырехчасовых работ, приведенные выше формулы для расчета погрешностей студенты должны были уметь выводить, а к готовым вариантам обращаться только для проверки. В условиях, когда сокращаются аудиторные часы, отведенные на изучение дисциплин, мы считаем целесообразным вооружить студентов таблицей со сводом формул, необходимых для вычисления погрешностей в частных случаях (см. табл.). Наиболее вовлеченные студенты смогут вывести эти формулы и дополнить данный перечень самостоятельно.
Свод формул для вычисления абсолютной и относительной погрешностей в частных случаях
A set of formulas for calculating absolute and relative errors in special cases

О целесообразности применения предложенного свода формул
Стоит отметить, что, ориентируясь в данной таблице, студенты могут быстрее выводить формулы для более сложных функций и во всех других курсах физики, изучаемых в НИУ МИЭТ.
Например, в лабораторной работе № 3 (Горбатый и др., 2015: 25; Спиридонов и др., 2021: 24) студенты изучают законы равно ускоренного движения на машине Атвуда. В одном из заданий необходимо вычислить ускорение груза по измеренной зависимости и найти погрешность для этого ускорения:
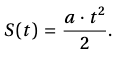
Во многих пособиях либо призывают студентов найти частные производные, либо приводят готовую формулу. В первом случае недостаточно подготовленный студент получает стресс и старается избежать самостоятельного выполнения работы. Во втором — отсутствует важная интеллектуальная/образовательная нагрузка, развивающая навык логических рассуждений, получения корректных выводов, не формируется культура работы с формулами, не развивается чувство структурной связи между частями сложных формул.
В случае применения таблицы формулу для вычисления абсолютной и относительной погрешности ускорения студент может получить следующим образом.
Для начала необходимо проанализировать уравнение:
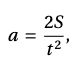
увидеть, что оно включает умножение и деление переменных и у одной из переменных присутствует степень. Сверившись с таблицей, студент должен увидеть сходство ситуации с вариантом из строки 3: при умножении и делении нескольких величин складываются их относительные погрешности. Сообразно установленному соответствию сначала удобно найти относительную погрешность, а затем абсолютную:
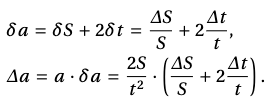
Из примера видно, что хотя функция и является функцией нескольких переменных, можно достаточно просто определить ее погрешность, избегая использования частных производных. Кроме того, появляется возможность проанализировать точность измерений величин, а также обсудить, какая из них дает больший вклад в погрешность.
Подведение итогов/Результаты и рекомендации
Применение в течение четырех лет предлагаемого нами подхода позволяет констатировать следующие положительные результаты:
- Подход способствует более глубокому усвоению материала и подготовке студентов к самостоятельной работе с экспериментальными данными.
- Студенты стали гораздо контактнее по отношению к преподавателю из-за ликвидации барьера, вызванного страхом неудачи/непонимания задачи.
- Студенты меньше априори переживают, что не поймут и не справятся, вследствие чего большее их число выполняет работу самостоятельно, реже встречается бездумное списывание.
При этом можем выделить ограничения по применению предлагаемого нами подхода.
Во-первых, методика, основанная на использовании здравого смысла, разумеется, оказывается в прямой зависимости от наличия у студента навыков логического рассуждения, формулировки выводов, чувства/понимания причинно-следственных связей. При наблюдаемом нами уровне освоения студентами дисциплины «Философия» и практически поголовно демонстрируемом ими затруднении с формулировкой выводов при отсутствии направляющих вопросов данное ограничение может оказаться существенным. В таком случае таблица со сводом формул будет особенно полезна.
Во-вторых, нововведения для официального изменения методов обучения требуют одобрения на многих уровнях, может потребоваться немало бюрократических процедур для официального признания и разрешения.
[1] Дмитриева Н. «Сегодня в технические вузы можно вовсе не сдавать ЕГЭ по физике». Интервью Н. Ивановой-Гладильщиковой. Вести образования: электронная газета. 27.06.2024. Web. 22.07.2025.
[2] «Вступительные испытания и минимальное количество баллов». Национальный исследовательский университет «МИЭТ»: Абитуриент: [сайт]. 22.07.2025.
[3] «Правила приема в МФТИ на обучение по образовательным программам высшего образования — программам бакалавриата в 2025 г.». Приёмная комиссия МФТИ: [сайт]. 22.07.2025.
[4] «111. Федеральная рабочая программа по учебному предмету “Математика” (базовый уровень)». Министерство просвещения Российской Федерации. Приказ от 18 мая 2023 года № 371 «Об утверждении федеральной образовательной программы среднего общего образования» (с изменениями на 19 марта 2024 года). III. Содержательный раздел. Консорциум «Кодекс»: Электронный фонд правовых и нормативно-технических документов: сайт. 23.07.2025; Институт содержания и методов обучения имени В. С. Леднева. «Федеральная рабочая программа среднего общего образования “Математика” (углубленный уровень) (для 10–11 классов образовательных организаций)». Единое содержание общего образования: сайт. 23.07.2025.
[5] «Премия. Драма». Реж. С. Микаэлян; СССР, киностудия «Ленфильм», 1974. Советский экран: видеозаписи: VK видео: [сайт]. 23.07.2025.
[6] К слову сказать, опыт обращения к советским учебникам для возврата к более простым и понятным для обучаемых объяснениям оказывается весьма востребованным в настоящее время — см. сообщество «Советские учебники» в социальной сети «ВКонтакте».
1. Andreyev A. D., Chernykh L. M. [Physics.] Processing of Measurement Results in Laboratory Physics Workshop: lecture notes. St. Petersburg: SPbSUT, 2009. 19 p. (In Russian)
2. Anisimov V. M., Danilova I. N., Pronina V. S., Solokhina G. E. Laboratory Work in Physics. Pt. 1. Mechanics. Molecular Physics and Thermodynamics. Ed. G. G. Spirin. Moscow: MAI, 2010. 236 p. (In Russian).
3. Belyankin A. G., Motulevich G. P., Chetverikova E. S., Yakovlev I. A., comp. Physical Practical Course. Mechanics and Molecular Physics. 2nd ed., rev. Ed. V. I. Iveronova. Moscow: Nauka, 1967. 352 p. (In Russian).
4. Boikov I. I., Harach O. G. “On Possibilities of Application of Neural Networks in the Training of IT Specialists in the Field of Programming at NIU MIET”. Aktual’nyye problemy informatizatsii v tsifrovoy ekonomike i nauchnykh issledovaniyakh: sb. statey IV Nauch.-prakt. konf. s mezhdunar. uchastiyem (Moskva, 23—24 noyabrya 2023 g.). Moscow: MIET, 2024. 9—26. (In Russian).
5. Bais S. The Equations: Icons of Knowledge. Cambridge, MA: Harvard Up, 2005. 96 p.
6. Golitsyna O. M., Merem’yanin A. V., Risin V. E., comp. Mathematical Processing of Measurement Results in Laboratory Practical Training on the Course of General Physics: teaching aid. Voronezh: VSU Publ. House, 2015. 20 p. (In Russian).
7. Gorbatyy I. N., Zykov A. V., Spiridonov A. B., Trifonov A. Yu. Laboratory Works on the “Mechanics” from the Course of General Physics: methodological manual. Ed. A. B. Spiridonov. Moscow: MIET, 2015. 180 p.: il. (In Russian).
8. Klepikov N. P. Translator’s Preface. Teoriya i praktika obrabotki rezul’tatov izmereniy. By L. Yanoshi. Transl. from English by N. V. Klepikov; eds. A. A. Gusev, E. S. Kuranskiy. 2nd ed. Moscow: Mir, 1968. 5—6. (In Russian).
9. Leont’yeva N. V., Lisitsyn S. G. A Collection of Laboratory Works on Physics. Mechanics: teaching aid. Moscow: NRNU MEPhI, 2015. 120 p. (In Russian).
10. Rusanov B. A., Sidorov V. Ye. Processing of Measurement Results in Laboratory Physics Practice: teaching aid for independent work of students. Yekaterinburg: USPU, 2023. 32 p. (In Russian).
11. Semenova F. O. “Professional Self-Consciousness of Boys and Girls in the Learning Process at the University — A Result of Opposition and Destructive Influence on Today’s Youth”. Psikhologo-pedagogicheskiye problemy sovremennogo obrazovaniya: puti i sposoby ikh resheniya: sb. materialov II Mezhdunar. nauch.-prakt. konf. (Derbent, 27 fevralya 2018 g.). Gen. ed. E. A. Pirmagomedova. N. p.: Parnas, 2019. 335—340. (In Russian).
12. Spiridonov A. B., Gorbatyy I. N., Zharinova N. N., Zykov A. V., Trifonov A. Yu. Laboratory Work on the “Mechanics” from the General Physics Course for Non-Physical Fields of Study: methodological manual. Ed A. B. Spiridonov. Moscow: MIET, 2021. 124 p.: il. (In Russian).
13. Stepanova Ye. A., Skulkina N. A., Volegov A. S. Fundamentals of Processing Measurement Results: [study guide]. Ed. Ye. A. Stepanova. Yekaterinburg: UrFU Publ., 2014. 95 p. (In Russian).
14. Tkachev V. A., Berestov A. T., Gorbatyy I. N., Ovchinnikov A. S., Romanov V. P., Shokina D. I. Laboratory Works on the General Physics Course. Mechanics. Moscow: MIET, 2003. 104 p. (In Russian).
15. Harach O. “About Ways to Avoid One of the Most Common SWOT-Analysis Mistake”. Innovatsionnyye podkhody k resheniyu tekhniko-ekonomicheskikh problem: sb. trudov konferentsii (Moskva, 25 noyabrya 2015 g.). Moscow: MIET, 2015. 106—111. (In Russian).
16. Cherbieva S. V., Bostanova S. N. “Empirical Study of Educational Stress Among the Students”. Uchenye zapiski universiteta imeni P. F. Lesgafta 12 (178) (2019): 445—451. (In Russian). https://doi.org/10.34835/issn.2308-1961.2019.12.445-451
17. Jánossy L. Theory and Practice of the Evaluation of Measurements. Oxford: Clarendon Press, 1965. 481 p.
18. Yashchenko E. F. “Interpersonal Conflict, Values, Strategies for Overcoming Stress Situations of Students Before and After the Start of a Special Military Operation”. Vestnik Universiteta 2 (2023): 212—220. (In Russian). https://doi.org/10.26425/1816-4277-2023-2-212-220








